La ordenación es un problema muy estudiado e interesante en el mundo de la computación. Es conocido que el problema de ordenación basado en comparaciones está resuelto en O(n*log(n)), es decir que se necesitan un mínimo de n*log(n) operaciones para ordenar un conjunto de n números.
Esta afirmación falta agregarle algunas cosas más para que sea del todo correcta. Por ejemplo, que no sabemos nada respecto al conjunto que queremos ordenar, y esto es importante ya que si tenemos información respecto del conjunto que queremos ordenar, podemos optimizar el tiempo de ordenación drásticamente.
Imaginemos que tenemos una lista de n elementos tales que a están en un rango de 1 a n, entonces es claro que podemos ordenar en tiempo lineal simplemente mostrando la lista {1,2,3,...,n}.
Ahora imaginemos que no son números enteros, son reales ¿cómo le haría Euclides para ordenar n números reales en tiempo lineal y sin computadora?
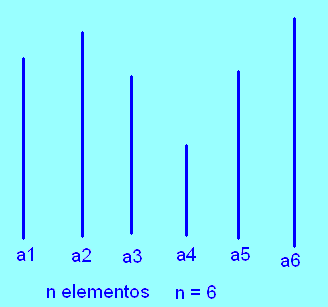
Ahora colocamos a los elementos uno encima de otros y los dejamos caer en la línea en el plano de 1 dimensión.

Se terminó, en tiempo lineal tenemos ordenado nuestro conjunto.
Esta afirmación falta agregarle algunas cosas más para que sea del todo correcta. Por ejemplo, que no sabemos nada respecto al conjunto que queremos ordenar, y esto es importante ya que si tenemos información respecto del conjunto que queremos ordenar, podemos optimizar el tiempo de ordenación drásticamente.
Imaginemos que tenemos una lista de n elementos tales que a están en un rango de 1 a n, entonces es claro que podemos ordenar en tiempo lineal simplemente mostrando la lista {1,2,3,...,n}.
Ahora imaginemos que no son números enteros, son reales ¿cómo le haría Euclides para ordenar n números reales en tiempo lineal y sin computadora?

Ahora colocamos a los elementos uno encima de otros y los dejamos caer en la línea en el plano de 1 dimensión.

Se terminó, en tiempo lineal tenemos ordenado nuestro conjunto.
1 comentario:
Ah, *tiempo* lineal, pero nada más ve cómo crece el espacio... formalmente eso es ordenamiento BeadSort, que permite no solamente tiempo lineal sino tiempo O(sqrt(n)). Pero usando gravedad (que es por naturaleza infinitamente paralelizable) y espacio en O(n²). Y como, por relatividad (y porque "espacio" aquí es espacio físico, no abstracto), espacio es equivalente a tiempo, para valores grandes de n ese O(n²) en espacio se va a "escurrir" también al tiempo.
Publicar un comentario